
Delivery planning and route optimization are vital for streamlining transport, labor and logistics costs in the era of free delivery and rising gas prices.
So called "last mile" deliveries can consume up to 30% of the entire supply chain cost so it's a prime candidate for optimization.
It's not without challenges. Even relatively simple route optimizations can be extremely complicated. Computers have a very difficult time trying to calculate efficient routes even for extremely short routes with simple delivery requirements.
Route optimizations are a famous example of the TSP (Travelling Salesman Problem).
Travelling Salesman Problem
The TSP has a simple formulation that asks the following question,
"Given a number of locations, what is the most efficient way to visit each one?"
Sounds easy.
The TSP is actually part of broader class of mathematical problem known as NP-Hard. These have a formal mathematical definition, but for our purposes the primary attribute that applies to delivery planning and route optimizations is as follows.
TSP Complexity
A small increase in the initial size of the TSP leads to a factorial increase (factorial growth is faster than exponential) in the number of potential solutions.
It's easier to understand this with an example.
Consider a salesman who need to visit 4 locations. What is the most efficient way to do this?
We could look at every possible route (permutation) and choose the best one. Initially we have 4 stops to choose from, then 3, then 2, then 1. Calculating the total gives us:
If we added only a single additional location, the calculation would be:
We can use shorthand for the series of multiplications using the mathematical operator called bang, denoted by an exclamation mark(!). So calculating a 6 stop TSP gives us:
It's easy to see that the number of possibilities grows extremely quickly for every additional location added to the initial problem. That's what makes route optimizations so difficult.
By the time you attempt to tackle real world problems the numbers are astronomical.
Consider a very small delivery company consisting of a single vehicle. It has to deliver packages to 50 locations on Monday. Working out how many possibilities there are is given by:
That's a lot of possibilities for a computer to check. Let's state this another way for perspective.
In the real world, companies tend to operate fleets of vehicles. By the time you attempt to tackle these problems the numbers become so astronomical as to be meaningless to humans. Consider the example of a small delivery company operating 5 vehicles with 100 locations to visit in a single day. The calculations for this problem are given by:
where V is the number of vehicles (5) and L is the number of locations (100). Plugging in these numbers gives us:
That number is so big we really need to wonder how long it would take a really fast computer to check each permutation in order to find the optimal route.
The SUMMIT supercomputer built by IBM for the Oak Ridge National Laboratory has the fastest processing capability in history (for now). This is measured in something called FLOPS, which stands for Floating Point Operations Per Second.
SUMMIT manages a respectable 200 petaflops. Peta denotes 10¹⁵, so we can write the number of petaflops from SUMMIT as 2 x 10¹⁷. Impressively fast.
Let’s be extremely generous and assume that a single flop is equivalent to a complete check of one possibility in our problem (it's not). Essentially, this means we could test 2 x 10¹⁷ possibilities every single second.
At 2 x 10¹⁷ checks per second we’re going to take:
Divide by the number of seconds in a minute, minutes in an hour, hours in a day, days in a year and we get:
That's a problem considering our best estimates for the remaining time left in the Universe stands at around 5 billion years, or 5 x 10⁹.
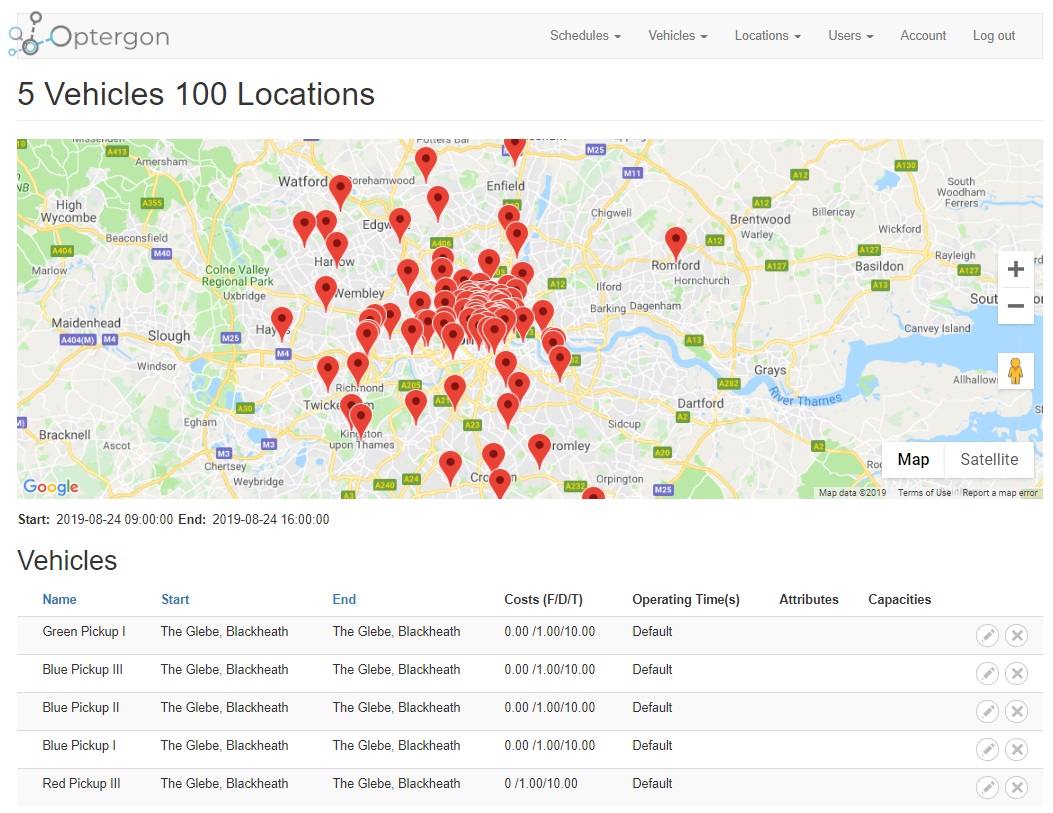
A 5 vehicle, 100 location problem looks like this on a map.
Running it through Optergon's heuristic algorithms gives the following optimized route solution (in under 1 minute).
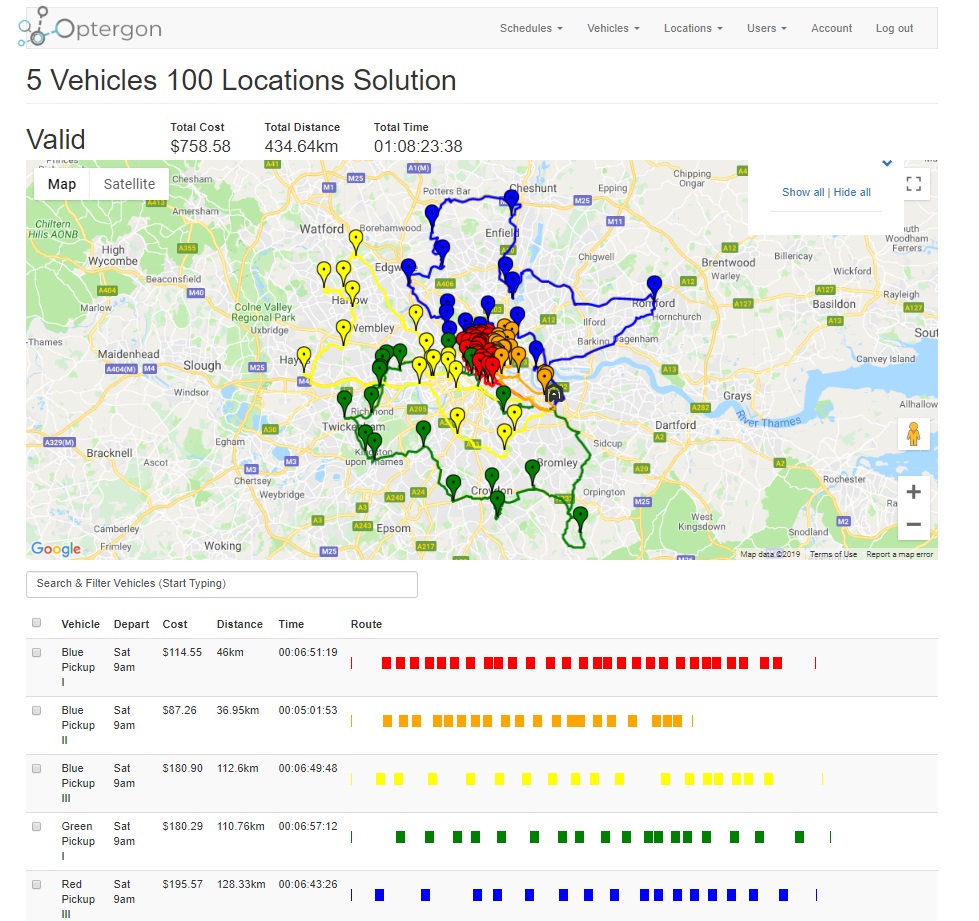
How is this possible given the astronomical number of permutation to check?
The answer lies in the phrase heuristic algorithm.
Heuristic Algorithm
A comparative process not guaranteed to produce a perfect result.
There are many examples of heuristic algorithms (many of which are taken from Nature). Here are a few well-known ones used by Optergon (in addition to several proprietary ones):
- Ant Colony Optimization: Mimics the behavior of ant colonies that emerge extremely efficient routes between the nest and outlying resources.
- Simulated Annealing: Mimics the effect of annealing - the process of repeatedly heating and tempering steel to improve its crystalline structure.
- Genetic Algorithm: Mimics how genes mutate and recombine to produce new individuals, well adapted for their environment.
Our brains are heuristic too. We don't calculate Newton's laws of motion when trying to catch a ball. Instead, our brains compare multiple remembered scenarios in order to make a best guess about how the ball will behave and where to position our hands.
That's why practice makes perfect. The more past scenarios our brains have to compare with the current situation, the better our heuristic guess will be.
Optergon can calculate optimal routes for hundreds of vehicles and thousands of locations because it "thinks" like a human brain. It doesn't have to brute force test every possible outcome because a very high number of those will not be efficient.
The downside is that it can't guarantee the best possible result because that can only be known by testing all possibilities (which puts us back to not having enough time left in the Universe).
However, unlike other systems that take all sorts of shortcuts to save on processing time (like dividing up the map into equal segments before optimizing several smaller individual routes), Optergon does some seriously heavy lifting in the background to produce better quality route optimizations and delivery planning schedules without using shortcuts.
This produces optimal delivery plans that are extremely difficult to improve. It's these high quality optimizations that save companies significant amounts of money on transport, fuel, wear and tear, labor, planning and logistics and a host of other costs up and down the supply chain.
